¿Cómo se determina la posición de las rectas en el plano por su función afín?

Si dos rectas presentan la misma pendiente, entonces serán paralelas, y se formarán dos ángulos congruentes entre la recta y el eje de las abscisas, como se observa en los siguientes gráficos:

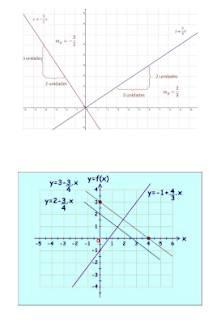
Si el producto de las pendientes de dos rectas da -1, entonces dichas rectas serán perpendiculares, como se observa en el siguiente gráfico:

Ejemplos

A) Determina si las rectas y = 6x + 5 ; y = 6x – 1 son paralelas.

1.-La pendiente de ambas rectas es 6.

2.-El punto de corte con el eje Y de la primera recta es (0, 5), y el de la segunda recta es (0, −1). No son la misma recta. Por lo tanto son paralelas.

 

 

B) Determinar si las rectas y = −8x + 5; y=1/8x-1 son perpendiculares.

1.- Se obtienen las pendientes de ambas rectas, a saber -8 y 1/8

2.- Se multiplican, dando -1

3.- Son perpendiculares

Ejercicios

http://www.vitutor.com/geo/rec/d_10_e.html

Lecturas  y videos adicionales de Interés 
https://es.khanacademy.org/math/geometry/analytic-geometry-topic/parallel-and-perpendicular/e/line_relationships

https://www.youtube.com/watch?v=gBkhlAxnE-U

Referencias

Matemáticatuya.com (s.f.) Rectas paralelas y rectas perpendiculares. Recuperado el 8 de febrero de 2016 de http://matematicatuya.com/GRAFICAecuaciones/S6.htmlv

Instituto de Monterrey (2011) Rectas paralelas y perpendiculares. Recuperado el 8 de febrero de 2016 de http://www.montereyinstitute.org/courses/DevelopmentalMath/TEXTGROUP-1-19_RESOURCE/U13_L2_T3_text_final_es.html