Función real
Desde
el punto de vista matemático, se dice que una función real es toda relación f
que asocia a cada uno de los elementos de cierto subconjunto de los
números reales (dominio o variable independiente) con otro subconjunto de
números reales (variable dependiente). También
ha sido expresada así: dados dos conjuntos X o dominio e Y codominio (diferentes
a vacío), una función real existe si el dominio de la relación es todo el
conjunto X (es decir que todos los
elementos de X tienen relación con un elemento de Y) y a cada elemento del
conjunto X le corresponde uno y solo un elemento del conjunto Y. Esta relación
se puede graficar en un plano cartesiano uniendo los pares ordenados (x,y), que
cumplen una función dada.
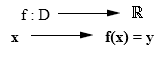
Matemáticamente
se expresa de la siguiente forma:
Gráficamente una función real se representa
así:
Función lineal
En el álgebra y la geometría, algunos autores llaman función lineal a aquella función afín con b = 0, y estas rectas pasan siempre por el origen de
coordenadas. La ordenada en el origen de
n es 0, es decir pasan por (0,0).
Matemáticamente se expresa como:
f(x) = mx
Gráficamente
se representa así:
Al compararla con la función afín, cuya
fórmula es y = m x + n donde m es la pendiente de la recta (grado
de inclinación). La
ordenada en el origen es n, punto donde la recta
corta al eje de ordenadas. Las coordenadas de este punto son (0, n). Es decir, la función afín tiene un coeficiente
independiente de la pendiente. Por lo
que, aunque técnicamente son lo mismo, mantienen una constante de
desfase ya que hay una constante (n) que hace que la recta deje de pasar por el
origen del sistema cartesiano.
Función constante
La función constante tiene como fórmula:
f(x)
= n
Donde n es una constante. La pendiente de la recta m = 0, no es ni
creciente ni decreciente. En el caso de esta función no es necesario hacer
tabla de valores porque la recta vale siempre y=n. La gráfica originada es una
línea horizontal paralela al eje x como se observa en la figura anexa.
Ejemplos
Determinar si las siguientes funciones son lineales, afines o constantes.
y = 2
constante
y = ¾ constante
y= 2x – 1 afín
y = −2x – 1 afín
y = x lineal
y = 2x lineal
Ejercicios
Lecturas y videos adicionales de Interés
Referencias
Huircan,
M. y Carmona, K. (2013) Guía de aprendizaje No 4: funciones lineales y afín. Recuperado el 6 de febrero de 2016 de http://portales.mineduc.cl/usuarios/adultos/doc/201404141136550.GuiaN4MatematicaICiclodeEM.pdf
Profesor
en línea (s.f.) Tipos de Función. Recuperado el 6 de febrero de 2016 de http://www.profesorenlinea.cl/matematica/Funciones_tipos.html



No hay comentarios:
Publicar un comentario